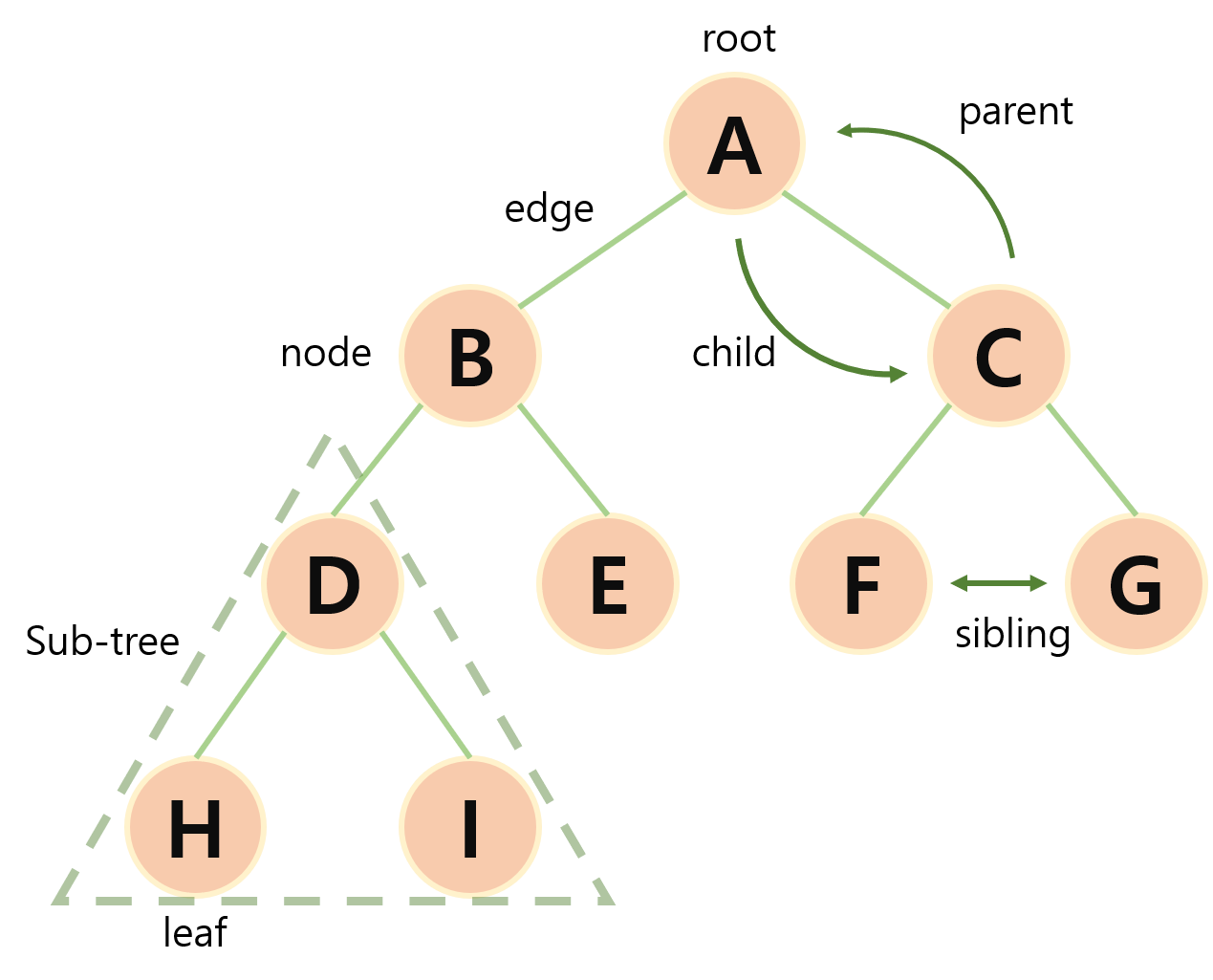
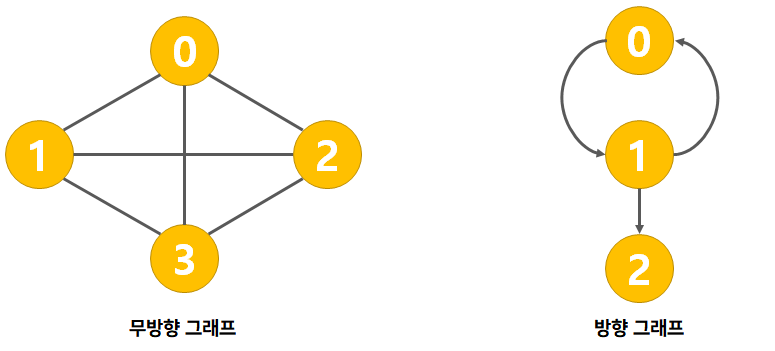
유니온 파인드란?
- 그래프 알고리즘 중 한 가지
- 분리 집합(상호배타적 집합)(Disjoing-set) 과 같은 알고리즘
- 여러 노드가 존재할 경우, 선택한 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘
- 위 과정이 Find, Union 두 가지 연산으로 이루어짐
Find : 노드 x 가 어떤 집합에 속하는지 확인하는 연산
Union : 노드 x와 y가 포함되어 있는 집합을 병합하는 연산
init함수
void init() {
for (int i = 1; i <= N; i++)
root[i] = i;
}- 모든 노드에 대하여 자기 자신을 자신의 root 로 초기화
Find함수
int find(int i) {
if (i == root[i])
return i;
else
return root[i] = find(root[i]); //경로 압축
}- 파라미터로 들어간 노드의 루트 노드를 반환하는 find 함수
- 어느 트리(집합)에 속해있는지를 확인하는 연산
- 한 쪽으로 트리가 치우쳐진 경우 트리로 구현하는 이점이 사라지기 때문에 경로 압축 최적화를 한다.
- 경로 압축 최적화 : i 에 대하여 루트 노드인 root[i]를 찾은 경우 i의 부모를 바로 루트 노드를 바꾸어 트리의 높이를 압축하여 find 함수의 효율을 높인다.
Union함수
void merge(int a, int b) {
int x = find(a);
int y = find(b);
//루트가 같다면 union과정 생략
if (x == y)
return;
if (rank[x] > rank[y])
root[y] = x;
else
root[x] = y;
//두 트리의 깊이가 같은 경우 y의 깊이를 늘림
if(rank[x] == rank[y])
++rank[y];
}- 집합을 함칠 때 높이가 더 높은 트리가 낮은 트리 밑으로 들어갈 경우 트리가 점점 깊어져 효율성이 떨어진다.
- rank 배열을 사용하여 트리의 높이가 낮은 트리가 높은 트리 밑으로 들어가도록 한다.
'알고리즘스터디' 카테고리의 다른 글
| [알고리즘] 트리 (Tree) (0) | 2021.01.04 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2020.12.09 |
| [알고리즘] 에라토스테네스의 체 (Sieve of Eratosthenes) (0) | 2020.11.19 |
| [알고리즘] 구간 합 (Prefix Sum) (0) | 2020.11.17 |
| [알고리즘] 백트래킹 (Backtracking) (0) | 2020.11.09 |