
동적 계획법 이란?
| 동적 계획법(動的計劃法, dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다. |
1. 조건
▶ 최적 부분 구조 : 기본 문제의 최적해가 부분 문제의 최적해를 포함하고 있는 구조 , 즉 전체 문제의 최적해가 부분 문제의 최적해들로써 구성이 되어있다는 것이다. 예를 들어 A 문제의 부분문제 a, b 가 있을 때 , a, b의 최적해가 a' , b' 라면 A의 최적해가 a' 와 b'로 구성되는 것을 증명한다면 이는 최적부분 구조를 가진다고 할 수 있다.
▶ 부분 문제 반복 : 재귀 알고리즘을 통해 문제를 해결할 때 같은 부분 문제를 계속 반복하여 해결해야 하는 경우 이를 부분 문제 반복 구조를 가진다 할 수 있다.
2. 방식
하나의 문제를 여러개의 하위 문제로 나누어 푼 다음 , 그것을 결합하여 최족적인 목적에 도달한다. 각 하위 문제에 대한 결과를 계산하여 , 이 결과들을 저장하고 같은 문제가 나왔을 경우 저장된 결과를 사용하여 해결한다. 이러한 방법을 통해 계산 횟수를 줄일 수 있다.
분할 정복(divide and conquer) 또한 큰 문제를 작은 문제로 나누어 해결하지만 동적 계획법은 작은 부분문제들이 반복되는 것을 이용하여 문제를 푸는 것이고 분할 정복은 작은 문제 내에서 반복이 일어나는 부분이 없다.
3. 이용
최단 경로 문제, 행렬의 제곱 문제 등의 최적화에 사용한다.
동적 계획법은 문제를 해결하기 위한 모든 방법을 검토하고, 그 중 최적의 풀이법을 찾아낼 수 있다.
문제에 대한 모든 방법을 충분히 빠른 속도로 처리할 수 있는 경우 최적의 해법이다.
4. memorization
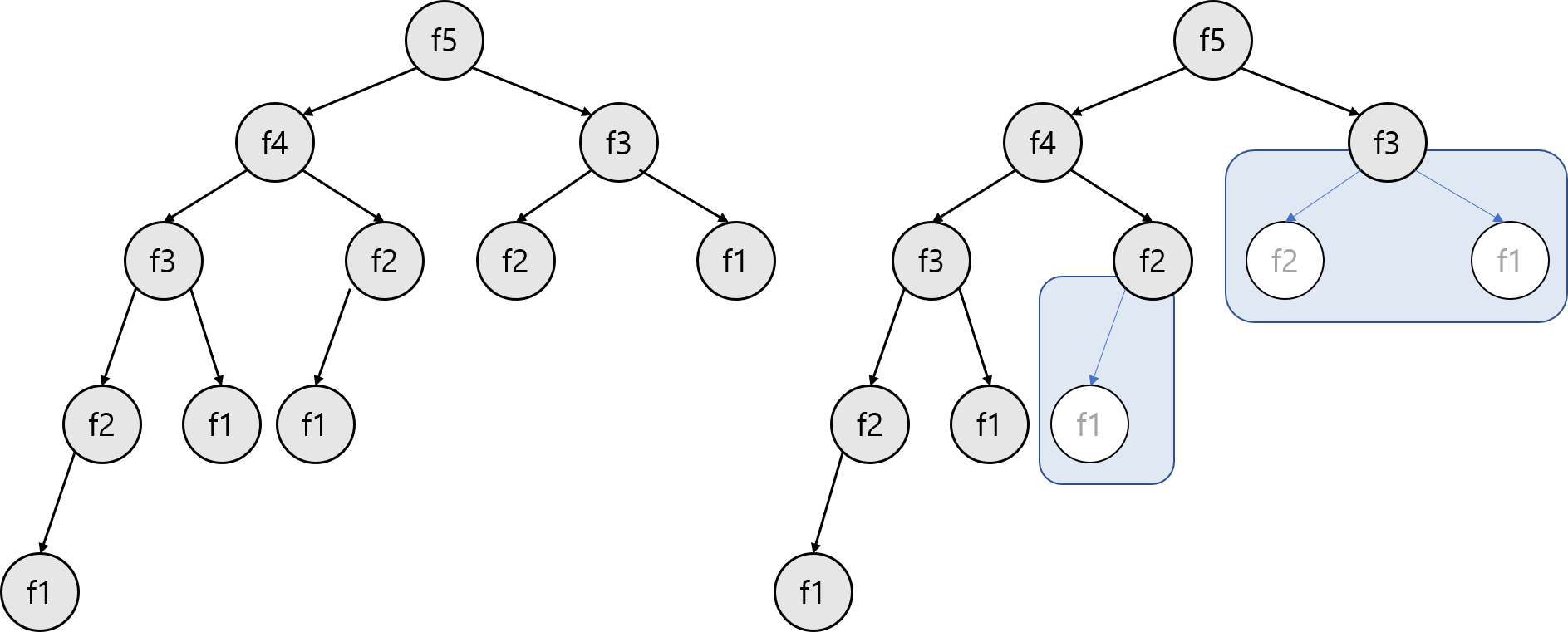
memorizaion을 사용하면 이미 한번 결과를 계산한 부분 문제에 대해서는 반복하여 계산하지 않는다.
위 피보나치 수열을 예로 들면 이미 계산한 f2->f1 과 f3->f2,f1 은 저장되어 있는 결과를 사용한다.
그렇기 때문에 전체 문제에 대한 총 계산횟수를 줄여주며 동적프로그래밍의 시간복잡도를 줄일 수 있다.
5. 관련문제
포도주 시식 [2156]https://www.acmicpc.net/problem/2156
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규
www.acmicpc.net
쉬운 계단 수 [10844] https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
팰린드롬 [10942] https://www.acmicpc.net/problem/10942
10942번: 팰린드롬?
총 M개의 줄에 걸쳐 홍준이의 질문에 대한 명우의 답을 입력으로 주어진 순서에 따라서 출력한다. 팰린드롬인 경우에는 1, 아닌 경우에는 0을 출력한다.
www.acmicpc.net
외판원 순회 [2098] https://www.acmicpc.net/problem/2098
2098번: 외판원 순회
첫째 줄에 도시의 수 N이 주어진다. (2 ≤ N ≤ 16) 다음 N개의 줄에는 비용 행렬이 주어진다. 각 행렬의 성분은 1,000,000 이하의 양의 정수이며, 갈 수 없는 경우는 0이 주어진다. W[i][j]는 도시 i에서 j
www.acmicpc.net
'알고리즘스터디' 카테고리의 다른 글
| [알고리즘] 깊이 우선 탐색 (DFS, Depth-First Search) (0) | 2020.10.27 |
|---|---|
| [알고리즘] 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2020.09.29 |
| [알고리즘] 분할정복 (Divide and Conquer) (0) | 2020.09.15 |
| [알고리즘] 탐욕법 (Greedy Algorithm) (0) | 2020.09.07 |
| [알고리즘] 완전 탐색 (Exhaustive search) (0) | 2020.08.31 |