[알고리즘] 에라토스테네스의 체 (Sieve of Eratosthenes)

수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.

 

 

에라토스테네스의 체는 소수를 구하기 위한 방법 중 하나로 프로그래밍 언어를 통해 알고리즘을 구현할 수 있다.

 

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
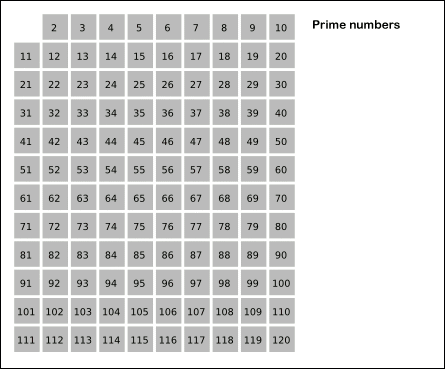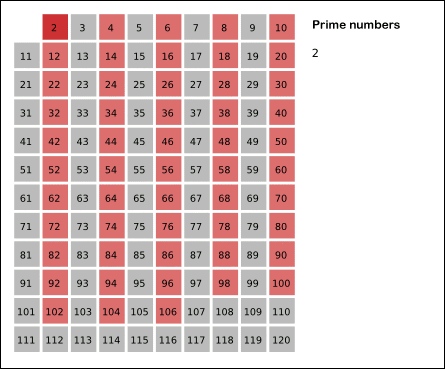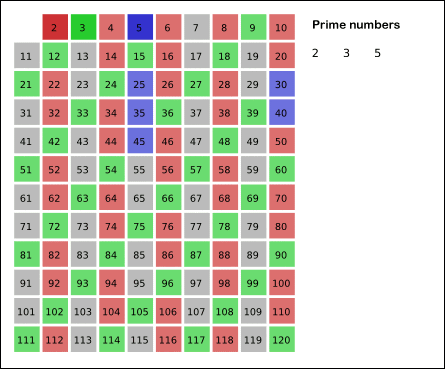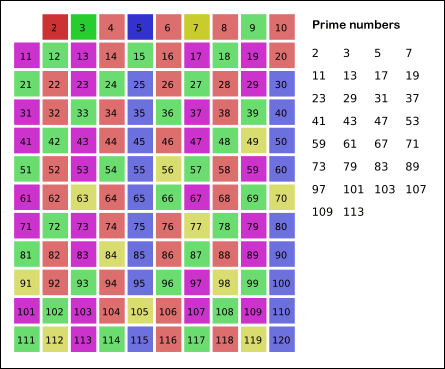
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.