기본 개념
-
버킷 정렬은 계수 정렬을 일반화 한 것으로 간주할 수 있다.
-
계수 정렬은 키 값이 작은 범위 안에 들어올 때 적용할 수 있는 방법이지만 버킷 정렬은 키 값의 범위뿐만이 아니라 그 범위 내에서 키값이 확률적으로 균등하게 분포된다고 가정할 수 있을 때 적용할 수 있는 방법이다.
-
키 값의 범위가 0과 1사이라고 가정할 때 n개의 키가 있을 때 구간 [0,1]을 n등분하고 이들 각각을 하나의 버킷으로 한다.
-
각 키를 크기에 따라 각 버킷에 분배하면, 키가 구간내에서 균등하게 분포한다고 가정했으므로, 하나의 버킷에는 하나의 키만 들어있을 확률이 높다.
-
한 버킷에 여러 키가 들어가게 된다면 같은 버킷에 속하는 키끼리는 간단한 정렬(삽입 정렬, 퀵 정렬 등)로 정렬한다.
-
이러한 버킷을 순서에 따라 출력하면 정렬된 결과를 얻을 수 있다.
버킷 정렬의 평균 실행시간은 O(n) 이다.
하지만 한 Bucket에 입력 키값들이 몰린 경우에는 버킷에 속하는 키들을 정렬하는 데 사용한 정렬의 시간복잡도 보다 오랜 실행시간이 소요된다.
그렇기 때문에 최악의 경우는 한 bucket에 키값들이 몰린 경우이며
최상의 경우는 각 bucket에 입력 키값들이 균등하게 분배된 경우이다.
과정
-
A배열에 10개의 데이터가 존재하므로 구간 크기가 0.1인 10개의 버킷 B를 만든다.
-
각 리스트 B[i] 에 대하여 퀵 정렬을 진행한다.
-
버킷에 저장되어있는 각 원소를 순서대로 출력하여 정렬을 완료한다.

코드
#define MAX 10 //배열의 개수 = 버킷을 등분할 개수
float A[MAX] = { 0.86,0.32,0.27,0.12,0.49,0.21,0.62,0.89,0.71,0.87 };
vector<float> B[MAX]; //버킷
bool desc(float a, float b){
return a > b;
}
void BucketSort()
{
for (int i = 0; i < MAX; i++)
B[(int)(A[i] * MAX)].push_back(A[i]); //A[i]를 B[n*A[i]]에 삽입
for (int i = 0; i < MAX; i++)
sort(B[i].begin(), B[i].end(),desc);
//STL Sort()를 이용하여 각 버킷 별로 정렬을 진행한다.
//N개로 나누어진 버킷에 있는 값들을 하나의 배열에 출력
int Idx = 0;
for (int j = 0; j < MAX; j++) {
while (B[j].empty() == 0) {
A[Idx] = B[j].back();
B[j].pop_back();
Idx++;
}
}
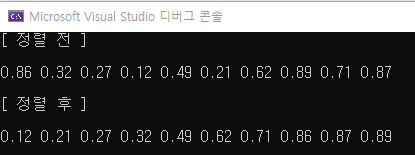
}결과
'알고리즘스터디' 카테고리의 다른 글
| [알고리즘] 탐욕법 (Greedy Algorithm) (0) | 2020.09.07 |
|---|---|
| [알고리즘] 완전 탐색 (Exhaustive search) (0) | 2020.08.31 |
| [알고리즘] 기수 정렬 (Radix Sort) (0) | 2020.08.26 |
| [알고리즘] 계수 정렬 (Count Sort) (0) | 2020.08.19 |
| [알고리즘] 힙 정렬 (Heap Sort) (0) | 2020.08.19 |