기본 개념
전체 키를 여러 자리로 나누어 각 자리마다 계수 정렬과 같은 안정적 정렬 알고리즘을 적용하여 정렬하는 방식이 기수 정렬이다.
그렇기 때문에 기수 정렬을 적용하기 위해서는 다음과 같은 조건이 필요하다.
- 입력 키들이 부동소숫점이 없는 정수여야 한다.
d 자리수 숫자들에 대하여 계수 정렬로 정렬한다면 각 자리에 대하여 O(n)이 걸리므로 전체로는 O(dn) 시간이 걸리고
d 를 상수로 처리한다면 기수 정렬은 O(n) 시간이 걸리는 알고리즘이다.
기수 정렬에는 LSD 와 MSD가 있다
1. LSD (Least Significant Digit) 방식 정렬
- 가장 작은 자릿수 부터 정렬을 진행
- 특징 : 가장 작은 자릿수부터 큰 자릿수까지 모두 비교해야 한다는 단점이 존재, 코드 구현이 MSD에 비해 간결하다.
2. MSD (Most Significant Digit) 방식의 정렬
- 가장 큰 자릿수 부터 정렬을 진행
- 특징 : 코드 구현은 LSD에 비해 복잡하지만(정렬 상태 확인 등) , 정렬 도중 중간에 정렬이 완료될 수 있다는 장점이 존재한다.
특징
모든 정렬 대상의 길이가 동일할 때 가장 효율적
입력 키들의 길이가 다를 경우 빈 공간을 메꾸는 추가 작업이 발생하여 성능이 저하된다.
- 좋은 예 {567, 654, 124, 457, 830, 911, 555} {dark, blue, high, best}
- 나쁜 예 {2154, 15, 54775, 1} {white, shy, h, strawberry}
계수 정렬을 이용한 정렬과정에서 전체 정렬 데이터 개수만큼의 메모리와 진법 크기 만큼의 메모리가 추가로 필요한 비제자리 정렬이므로 메모리의 여유가 많지 않는 경우에는 적용하기 어려운 정렬 방법이다.
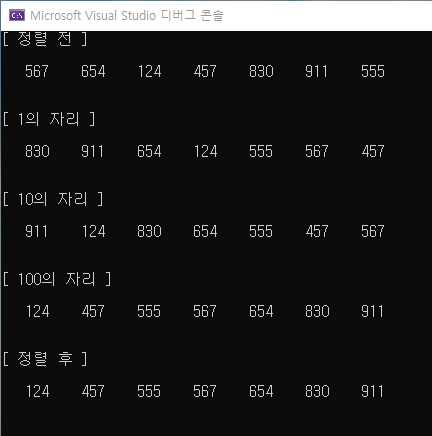
과정

코드
int maxValue; // 최대 자릿수를 계산하기 위해 최댓값 저장
queue<int> Q[10]; //0-9에 대한 버킷
void Radix_Sort()
{
int radix = 1;
while (1){ // 최댓값을 활용하여 최대자릿수를 구함
if (radix >= maxValue) break;
radix = radix * 10;
}
//1의 자리부터 최대자릿수까지 과정 반복
for (int i = 1; i < radix; i = i * 10){
for (int j = 0; j < sizeof(arr) / sizeof(arr[0]); j++){ //배열 전체 탐색
int K;
if (arr[j] < i) K = 0; //현재 탐색중인 자릿수보다 작으면 K는 0
else K = (arr[j] / i) % 10; // 다른 경우에는 현재 자릿수에 해당하는 숫자 K를 구함
Q[K].push(arr[j]); //해당하는 Queue에 push
}
int Idx = 0;
//0부터 9 까지의 Queue에 저장된 값들을 순차적으로 배열에 저장
for (int j = 0; j < 10; j++){
while (Q[j].empty() == 0){
arr[Idx] = Q[j].front();
Q[j].pop();
Idx++;
}
}
}
}결과
'알고리즘스터디' 카테고리의 다른 글
| [알고리즘] 완전 탐색 (Exhaustive search) (0) | 2020.08.31 |
|---|---|
| [알고리즘] 버킷 정렬 (Bucket Sort) (0) | 2020.08.26 |
| [알고리즘] 계수 정렬 (Count Sort) (0) | 2020.08.19 |
| [알고리즘] 힙 정렬 (Heap Sort) (0) | 2020.08.19 |
| [알고리즘] 쉘 정렬 (Shell Sort) (0) | 2020.08.10 |