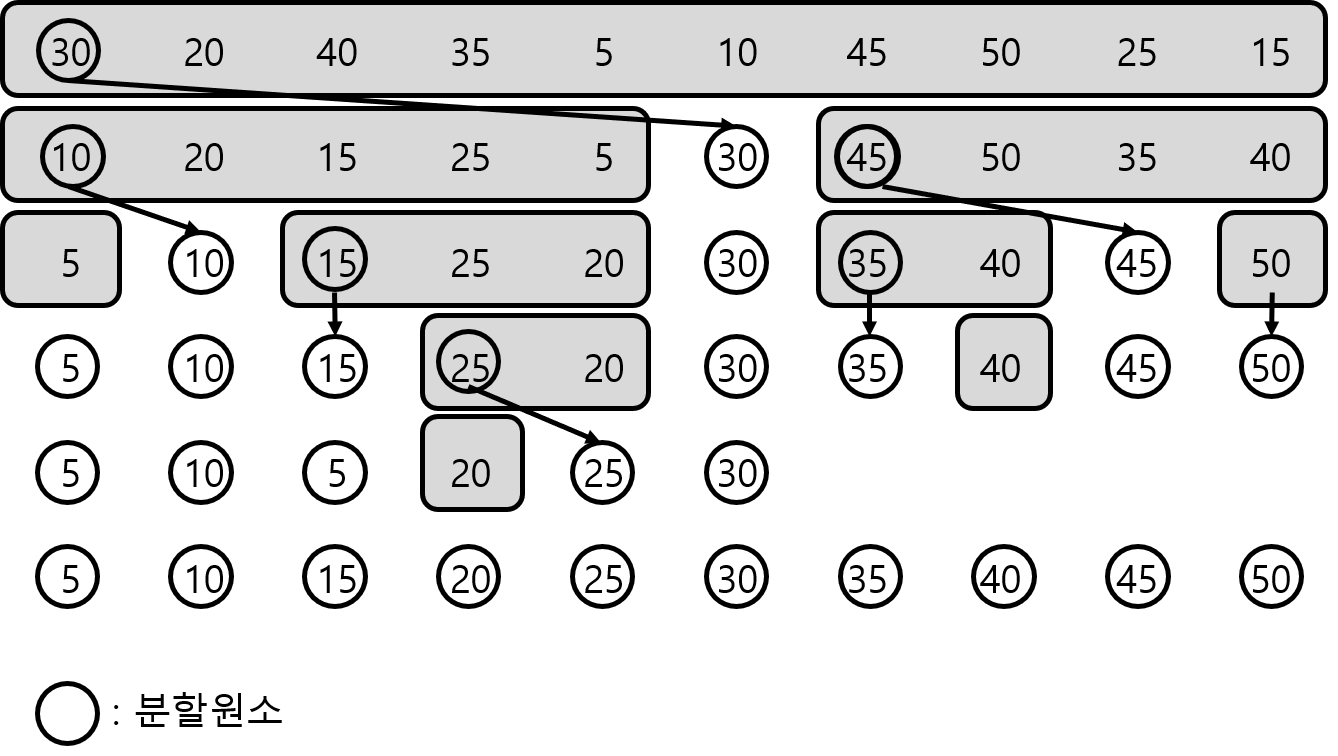
기본 개념
- 정렬할 키들을 배열 내에서 적당히 이동시키면서 두 조건이 만족되도록 배열을 오른쪽 부분 배열과 왼쪽 부분배열로 나눈다.
- (1) 왼쪽 부분배열에 있는 모든 키들은 오른쪽 부분배열의 가장 작은 키보다 작다.
- (2) 오른쪽 부분배열에 있는 모든 키들은 왼쪽 부분배열의 가장 큰 키보다 크다.
- 배열을 이렇게 나누면, 앞으로의 정렬 과정에서 왼쪽 부분배열의 키들과 오른쪽 부분배열의 키들이 전혀 섞이지 않게 된다.
- 이 점을 이용하여 왼쪽 부분배열과 오른쪽 부분배열에 독립적으로 퀵 정렬을 순환적으로 적용함으로써 배열 전체를 정렬할 수 있다.
정렬할 배열을 두 개의 부분배열로 나누는 방법
- 배열에서 임의의 키를 선택하여 이를 분할 원소라 한다.
- 분할하고자 하는 배열을 양끝으로부터 배열의 중심을 향하여 동시에 검색하여 간다.
- 왼쪽에서 오른쪽 방향으로 검색할 때는 분할 원소보다 큰 키를 찾는다.
- 오른쪽으로부터 왼쪽을 향하여 검색할 때는 분할 원소보다 작은 키를 찾는다.
- 이 두 키의 자리를 서로 바꾸고 검색을 계속한다.
- 검색 과정에서 이와 같은 조건을 만족하는 키들이 또 나타날 때마다 이들의 자리를 서로 바꾼다.
- 양끝에서 중심을 향하여 진행하던 검색이 배열의 어느 곳에서 서로 만나게 되면 검색을 끝내고 그 자리에 분할 원소를 넣는다.
- 이렇게 되면 분할 원소는 제자리를 찾는다.
- 분할 원소의 왼쪽에 있는 모든 키들은 분할 원소보다 작고, 오른쪽에 있는 모든 키들은 분할 원소보다 크다는 조건을 만족한다.
시간복잡도
Worst Case
ex> 분할 원소 하나만 제자리를 잡고 나머지 원소 모두가 왼쪽 혹은 오른쪽 부분 배열로 되는 경우
-> 1, 2, 3, 4, 5, 6, 7, 8, 9 (이미 제 순서로 된 경우)
-> 9, 8, 7, 6, 5, 4, 3, 2, 1 (역순으로 된 경우)
n+(n−1)+(n−2)+...+1=O(n2)
Best Case
ex> 분할 원소를 중심으로 두 부분 배열이 정확히 둘로 나뉘는 경우
2T(n/2) +n
=4T(n/4) + 2(n/2) + n
=8T(n/8)+n+n+n
=....
=n+nlgn
=O(nlogn)
Average Case
Partition 함수
int Partition(int A[], int left, int right)
{
int partElem, value, temp;
partElem = left;
value = A[partElem];
//left와 right가 교차할 때까지 반복
do {
//A[left]가 분할원소값보다 작으면 left를 반복증가시킴
do { } while (A[++left] < value);
//A[right]가 분할원소값보다 크면 right를 반복감소시킴
do { } while (A[--right] > value);
//두 값을 교환
if (left < right) swap(A[left], A[right]);
else break;
} while (left<right);
//분할원소의 자리를 찾아줌
A[partElem] = A[right];
A[right] = value;
return right;
}QuickSort함수
void QuickSort(int A[], int left, int right)
{
if (right > left)
{
int middle = Partition(A, left, right + 1);
//분할원소를 기준으로 왼쪽에서 재정렬
QuickSort(A, left, middle - 1);
//분할원소를 기준으로 오른쪽에서 재정렬
QuickSort(A, middle + 1, right);
}
}
'알고리즘스터디' 카테고리의 다른 글
| [알고리즘] 힙 정렬 (Heap Sort) (0) | 2020.08.19 |
|---|---|
| [알고리즘] 쉘 정렬 (Shell Sort) (0) | 2020.08.10 |
| [알고리즘] 삽입정렬 (Insertion Sort) (0) | 2020.08.03 |
| [알고리즘] 버블정렬 (Bubble Sort) (0) | 2020.08.03 |
| [알고리즘] 선택정렬 (Selection Sort) (0) | 2020.08.03 |